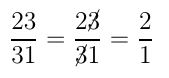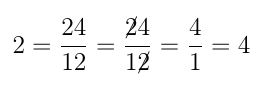Divisibility Rules (3 and 9)

In this blog series, I am exploring a few of my favourite algorithms in mathematics.

Last week, we looked at an algorithm that allowed us to calculate the greatest common divisor of two numbers using halving and subtraction. This week, I want to dive into the idea of divisibility rules.

Some numbers have easy divisibility rules. For example, a number is divisible by 2 if it ends in a 0, 2, 4, 6, or 8. It doesn’t take much mental energy to confirm that is indeed divisible by 2. Similarly, a number is divisible by 5 if it ends in a 0 or 5. So clearly is not divisible by 5.

But what about 3? Is divisible by 3? Perhaps numbers that are divisible by 3 have a nice pattern, like the numbers that are divisible by 2 or 5. If we start at 3, and list all numbers divisible by 3, we get:

This list is not good news. Notice that these numbers end in every possible digit! So is divisible by 3? Well it ends in a 5, let’s consider our options.

15 is divisible by 3 and ends in a 5. But 25 also ends in a 5 and clearly 25 is not divisible by 3. Ending in a 5 is not enough to determine divisibility by 3. So all we can say is maybe, maybe divisible by 3…

This illustrates a very crucial fact: to determine divisibility by 3, we need to look beyond the last digit of the number. Indeed, in the divisibility rule for 3, all the digits in the number will play a role.

The first step is to forget about the place value of each of these digits and simply treat them as individual numbers. Next, we add up all these numbers. For , this gives us:

Now we ask a surprising question, is this new number divisible by 3? For sure! 24 is on our list of numbers divisible by 3. So the rule says, since this new number is divisible by 3, the original number is divisible by 3. Done.

Don’t believe me? Calculate . You will get back our number:

Let’s try a smaller number. Clearly is divisible by 3 since . If we use our rule, we get:

Since 12 is divisible by 3, is also divisible by 3.

We can even apply this rule multiple times. Consider the gigantic number . Is this number divisible by 3?

First, we add all the digits:

Now 54 is not on our list. We could try some mental math to determine if 54 is or is not divisible by 3, but instead, we can just add the digits again!

9 is on our list and we are done, is divisible by 3.

To see why this works, consider . If we apply our algorithm, we get

This means should divisible by 3 according to our rule.

Now let’s unpack what we did. The first 2 actually stands for 2 groups of 1000, the 7 stands for 7 groups of 100, the 8 stands for 8 groups of 10, and the last 4 stands for 4. We could write this as:

Next, we break off a 1 from each of these powers of 10. This give us:

Finally, we can use the distributive property and get:

Now won’t affect our final answer because 999 is already divisible by 3. Similarly, and also wont affect our final answer. If we discard all these terms, we get:

This is just adding up all the digits, exactly what we were doing! In essence, by only using the digit and not the place value, we are disregarding either a 9, or a 99, or a 999. But these numbers are already divisible by 3 and so disregarding them is totally fine.

As a fun extension, this rule also works for divisibility by 9. So, our first number is not divisible by 9, since 24 is not divisible by 9. However, our gigantic number, is divisible by 9, since 54 is divisible by 9.

I love both of these divisibility rules because they employ such simple mathematical operations. Trying to do long division on a number like would be a very tedious process. But anyone can add up the digits of a number. And you could even have fun doing it!

GCD Algorithm

GCD Algorithm

In this blog series, I am exploring a few of my favourite algorithms in mathematics.

Last week, we looked at an algorithm that allowed us to perform multiplication using just doubling and addition. This week, I want to look an algorithm that enables us to calculate the GCD of two numbers using only halving and subtraction.

What is the GCD you might ask? The acronym stands for ‘greatest common divisor.’ As the name suggests, we first need to find all the common divisors of two numbers. For example, for the numbers 12 and 30, some quick mental math will show that 1, 2, 3, and 6 all divide evenly into both numbers. That makes 1, 2, 3, and 6 common divisors. And which one is the largest? 6 of course. Hence, 6 is the GCD of 12 and 30.

This task is relatively easy to do in your head when the numbers are small. What is the GCD of 15 and 50? After a bit of thinking, you should come up with the correct answer of 5.

However, the task is much more difficult with larger numbers. What is the GCD of 1980 and 306?

Both numbers are even, so we know the GCD must be at least 2. But what else can we say?

Well, let’s use that evenness of both numbers to our advantage and cut both numbers in half. That gives us two new numbers:

Now one of the numbers is even and one is odd. In this case, we just cut in half the even number and leave the other number alone.

Now both numbers are odd. What can we do? We can’t cut either number in half because odd numbers don’t divide in half… that’s what makes them odd!

The trick is to subtract the numbers. When you subtract an odd number from an odd number, you get an even number! Also, we always need to keep two numbers as we perform this algorithm, so let’s also keep the smaller number. Since , this means we have:

Alright, we got ourselves an even number, let’s go ahead and cut it in half.

.

Again, two odd numbers. So perform subtraction, , and this gives us:

Continuing with this process, we get:

(Halve it)

(Subtract em)

(Halve it)

(Halve it)

(Halve it)

(Done!)

Now both numbers are the same. Well, the greatest common divisor of 9 and 9 is of course 9. And don’t forget that 2 from the first step when both were even. Combining these facts gives us:

Tada! We found the GCD. You can check for yourself if you don’t believe me: https://www.wolframalpha.com/input/?i=gcd%281980%2C+306%29

What I find so wonderful about this algorithm is that we only need the skills of halving and subtracting. Both skills can even be done mentally, making this algorithm extremely quick when a calculator is not available.

Go ahead and try it out yourself, calculate the GCD of 238 and 136. You can check your answer here when you finish: https://www.wolframalpha.com/input/?i=gcd+%28238%2C+136

This algorithm, published by Josef Stein[1], works because of two important facts about divisors. First, when one number is even and one odd, the number 2 can divided out by halving the even number. This halving step won’t affect the final answer because an even and an odd number clearly do not share the number 2 as a common divisor.

Second, when both numbers are odd, a quirk of divisors allows us to replace the larger number with the difference of both numbers. Again, this replacement will not affect the final answer.

Using these two insights over and over allows us to shrink the numbers until they equal each other, at which point, we have found the number they both have in common.

---

[1] https://en.wikipedia.org/wiki/Binary_GCD_algorithm#:~:text=The%20binary%20GCD%20algorithm%2C%20also,shifts%2C%20comparisons%2C%20and%20subtraction.

Multiplication Algorithm

An algorithm is a series of steps that allows you to solve a problem. Over the next few weeks, I want to explore a few of my favourite algorithms in mathematics.

To start, consider . You could your hand at long multiplication to find the answer. However, I want to show you a more interesting method, an algorithm you probably never learned in school.

Create two columns. On the left side start with 1 and on the right side start with our second number, 31. Next, double each entry as you go down the column. The left side is easy, 1, 2, 4, 8, 16. The right side takes a bit more work, but you get the following:

1	31
2	62
4	124
8	248
16	496

Believe it or not, these two columns contain all the information we need to solve our multiplication question. We just need to find a way to make 29 using only the numbers in our left column. Can you see it?

1	31
2	62
4	124
8	248
16	496

Ok, now look at the numbers in the right column that correspond to the numbers we just found. Go ahead and added up these four numbers and see what you get.

1	31
2	62
4	124
8	248
16	496

If you were careful with your addition, you should have: which is the correct answer to: . Remarkable!

As a side note, I was not the first person to discover this. The credit for this method of multiplication goes all the way back to the ancient Egyptians.[1]

The reason this algorithm works is that we have broken down the large multiplication question into a series of smaller multiplication steps. The first row of the table states that 1 group of 31 equals 31. The second row of the tables shows that 2 groups of 31 equals 62. The third row shows that 4 groups of 31 equals 124. And so on. To get to 29 groups of 31, we notice that . This allows us find precisely 29 groups of 31, add them together, and get our total of 899.

Go ahead an try the algorithm out for yourself. Maybe compute . You can use the same table, and I bet you will get 589.

Now you might wonder, will this always work? What if I needed to calculate ? There seems to be no way to get to 35 using only the numbers in the left column…

Well, no worries, just add another row!

1	31
2	62
4	124
8	248
16	496
32	992

We can get to 35 no problem, just take 32, 2, and 1. In fact, the numbers in the left column, the powers of 2, have the unique property that you can get to any number you want, just by finding the right combination. Amazing! Those Egyptians were really on to something.

---

[1] https://en.wikipedia.org/wiki/Ancient_Egyptian_multiplication

Equals Sign

Everyone has their own little pet peeves. Some people need to load the dishwasher the same way each time, others insist on straightening other people’s picture frames. Well, as a math educator, there is one math error that drives me up the wall. The inability to use the equals sign.

Consider the popular Ed Sheeran song “Beautiful People.” At the time of writing, the music video for this song has over 62 million views. And yet… consider this screenshot from the video:

Ed Sheeran is trying to figure everything out in life, a noble goal. Except, neither him, nor his editors, can figure out how to use the equals sign! Can you spot the mistake? Apparently, everyone involved with this video believes that .

Now, everyone should agree that . This is a correct mathematical statement. Of course, one and one gives two.

Likewise, . This is also a correct mathematical statement. Two groups of three will produce a total of six.

However, to combine both statements together gives the completely nonsensical conclusion, that .

Part of the reason I think this error is popular, I mean it made it into a famous music video, is that calculators work different than math is written. If you type into your calculator it will give you the number . Then, you can go ahead and type and the calculator will happily give you the number .

The calculator is designed for what I call ‘process’ math. Perhaps you are in the process of adding up your grocery bill, so you add a few prices, then maybe you multiply by tax, then maybe there is a 10-dollar discount, and so on. So in the calculator case, the equals sign functions as a ‘process’ or as the next step as you keep track of items, tax, and discounts. Your claim isn’t that the first thing was equal to the last thing. Far from it. Your goal, as you continually press the equals sign, is to determine how much your final bill will be.

But when you actually write out all the equals sign on paper, it takes on a very different meaning. The sign literally means that whatever is to the left of it, and whatever is to the right of it, must be equal, identical, equivalent. So in the music video, because there are multiple equals signs, Ed Sheeran is claiming that

So Ed, if you are reading this, a better way to write your math would be:

“We’re just trying to figure everything out”

I know it takes an extra line, but it makes me feel better. Thanks.

Freaky Fraction Cancelling

As a follow up to my last post, take the example of ‘cancelling,’ a common technique in algebra. A student may be asked to simplify the fraction:

Instead of actually calculating 13 times 20, and then dividing by 20, a clever student may instead ‘cancel’ the 20 on the top and the bottom giving a final answer of 13. This can also be done with more complicated fractions. For example:

Since , we can cancel the 25 on the top and bottom to leave us with the much simpler expression:

However, my students often do not understand the limits of this cancelling technique. For example, they may think that in the fraction

the 3’s can be cancelled and reduce the fraction to

This leads to a whole mess of confusions.

Instead, we will start with the statement ‘you can always cancel any number on the top and bottom of a fraction.’

Next, a few choice examples make this rule seem plausible:

 

We can check that each example is valid by comparing the decimal representations on a calculator. Sure enough, the initial and final fractions are the same. The students now think that the rule is true. While they have not proved it, emotionally, they are sold on the technique. They believe it.

It is at this moment we create a shocking counterexample:

Everyone knows that 2 is not equal to 4. But our method has produced just that. Thus, our method is incorrect. The statement ‘you can always cancel any number on the top and bottom of a fraction’ must be false.

Of course you can sometimes cancel numbers and get the correct answer. But math is not about sometimes. If we state a general rule, it should hold all the time. By exhibiting a counterexample where the rule fails, and doing so with an emotional shock, hopefully students will not attempt to follow the misguided rule.